Readme

参考书：《数学模型（第四版）》姜启源

目的：备战国赛

updated：估计就去打打酱油hhh，毕竟没怎么认真学

第1章建立数学模型

基本概念

原型：人们在现实世界里关心、研究或者从事生产、管理的实际对象。

模型：为了某个特定目的将原型的某一部分信息简缩、提炼而构造的原型替代物

原型有各个方面和各种层次的特征，而模型只要求反映与某种目的有关的那些方面和层次。

模型：

物质模型/形象模型：
- 直观模型：把原型的尺寸按比例缩小或放大
- 物理模型：可显示原型的外形或某些特征，也可以用来进行模拟实验，间接研究原型的某些规律
理想模型/抽象模型：
- 思维模型：如司机对方向盘的操纵等
- 符号模型：在一些约定或假设下借助专门的符号、线条等，按一定形式组合起来描述原型。如地图等
- 数学模型：由数字、字母或其他数学符号组成，描述现实对象数量规律的数学公式、图形或算法

数学模型：对于现实世界的一个特定对象，为了一个特定目的，根据特有的内在规律，作出一些必要的简化假设，运用恰当的数学工具，得到的一个数学结构。

基本方法&一般步骤

基本方法

1.机理分析：找出反映内部机理的数量规律

2.测试分析：将研究对象看作一个“黑箱”系统（即内部机理看不清楚），通过对系统输入、输出数据的测量和统计分析，按照一定准测找出与数据拟合得最好的模型

通常采用两种方法结合起来进行建模，即用机理分析建立模型的结构，用测试分析确定模型的参数

一般步骤

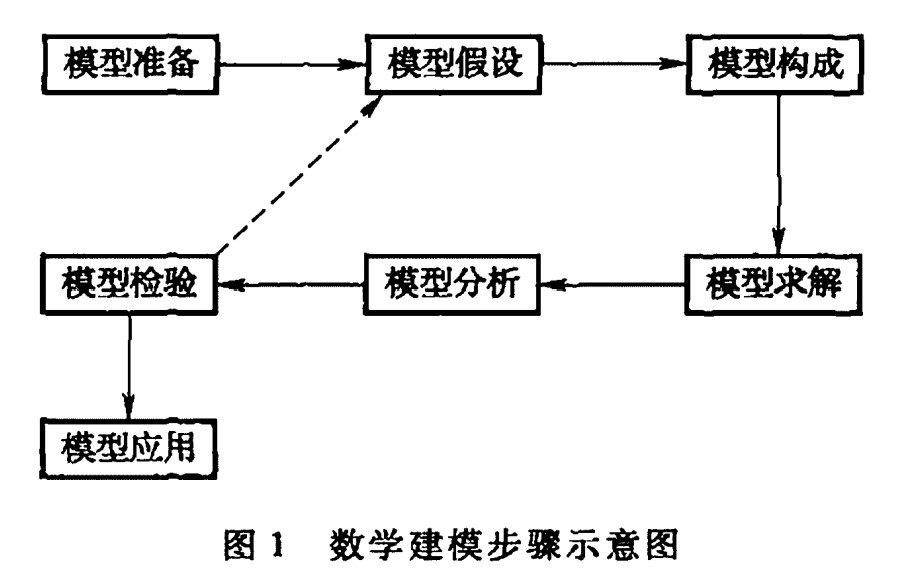
模型准备：了解问题的实际背景，明确建模目的，搜集资料
模型假设：抓住问题本质，作出并简化假设
模型构成：根据假设，采用数学的语言建立模型
模型求解：可以采用解方程、画图形、优化方法、数值计算、统计分析等各种数学方法，特别是数学软件和计算机技术
模型分析：对求解结果进行数学上的分析，如结果的误差分析、统计分析、模型对数据的灵敏性分析、对假设的强健性分析等
模型检验：回到实际问题。若结果不符，则通常是模型假设有误。
模型应用：应用方式等

即将实际问题抽象成数学模型，经过计算后得到模型的解答，再拟合实际问题

第2章初等模型

研究对象机理较简单，采用静态、线性、确定性模型描述就能达到建模目的。

2.1光盘的数据容量

模型准备

1.盘片上环形区域面积一定时，数据信息容量的大小取决于信道的总长度与信道上存储数据的线密度。而二者又取决于激光波长和驱动光盘的机械形式。

2.由于光的衍射作用，激光束会形成光斑。光斑大小与激光波长成正比，线密度与光斑大小成反比。

3.驱动光盘的机械形式分为两种：恒定角速度CAV和恒定线速度CLV

CAV：转速固定，每一圈螺旋线上要储存同等数量的数据信息。故由内向外，线密度递减。信息容量取决于螺旋线最内圈的长度、线密度以及总圈数。
CLV：线速度固定，线密度不变。信息容量取决于固定的线密度和螺旋线总长度。

模型建立

螺旋线的长度：

用同心圆周长之和来近似
用环形区域面积除以信道间距
用同心圆平均周长乘以总圈数

2.2双层玻璃窗的功效

简单的高中物理热学知识

2.3划船比赛的成绩

分析

以研究目的为中心，找相关的影响因素。

比如建模目的是寻求桨手数量与比赛成绩之间的数量规律。

影响因素是阻力，影响阻力的因素有桨手数、桨手体重、划桨功率、船速等等。

模型假设：

艇的静态特征（艇的几何形状，艇重与桨手数的关系）、动态特征（船速，阻力），其他因素（桨手体重，每个桨手的划桨功率）

模型检验

一般是将实际数据代入模型中看是否吻合

2.4实物交换

采用无差别曲线，利用图形方法建立实物交换模型的基础。

确定曲线需要大量的数据。

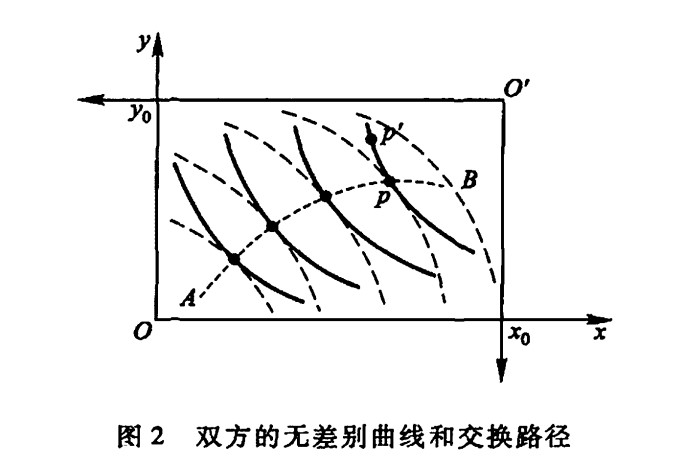
some thoughts：如果双方交换的物品是三种，可否提出无差别曲面的概念？

2.5污水均流地的设计

2.6交通流与道路通行能力

流量q：辆/h
速度v：km/h
密度k：辆/km

一般认为三者为常数，且q=vk

模型一

Greenshields提出速度与密度之间存在线性关系：
$$
v=v_f(1-k/k_j)
$$
v_f是密度为0时的车速，即理论上的最高车速，称为畅行车速

k_j是速度为0时的密度，称为阻塞密度

适用于密度适中的情况

带入上述公式，可得到流量与密度的关系，为一条抛物线。最大流量出现在畅行车速的一半处

模型二

对数模型，适用于密度较大的情况
$$
v=v_1ln(k_j/k)
$$

模型三

指数模型，适用于密度较小的情况
$$
v=v_fexp(-k/k_j)
$$

2.7核军备竞赛

也是建立图的模型

采用最小逼近方法

2.8扬帆远航

简单的物理速度分解知识以及没学过的流体力学知识

2.9天气预防的评价

第三章简单的优化模型

首先确定优化的目标是什么，寻求的决策是什么，限制条件，用什么数学工具（变量、常数、函数等）表示，怎样简化假设等等

3.1存贮模型

不允许缺货的存贮模型

经济订货批量公式（EOQ公式）

允许缺货的存贮模型

将假设3改为：每天每件产品缺货损失费为c_3

3.2生猪的出售时机

敏感性分析和强健性分析：本质是模型需要考虑到现实中的各种因素，不能过于理想化。